这篇文章来自于一个错误。在分析"拼手气红包"先后领取的金额分布的不同时,因为做出了错误的假设,使得推导出的先后领取红包的期望金额远远不同。这不符合实际“拼手气红包”的情况。但这意外地成了“拼手速红包”,最后还有蛮漂亮的数学结果,就还是记录了下来。( @毕导做过正确的分析,在文末有链接)(什么?你问我为什么放到文末?)
因为文中需要第三人称,所以就用了超级喜欢的《小绿与小蓝》的背景,OOC勿喷。毕竟小蓝在这里只是推进演绎的工具人(狗头)
快过年了。
看着走在身边的小蓝,我不禁想到:“小蓝,拼手气红包里的金额是怎么随机出来的?”
“当我们轮流抢红包的时候,每次可以看成是从剩余的钱中获得一定比例的钱,我们可以从这个比例所服从的概率分布入手。假设这个分布是均匀分布!”,小蓝说,“我算一下…”
在小蓝计算的时候,我们不妨先直观地分析一下,既然是拼手气红包,那影响钱数的应该只有运气。无论你是第几个抽到红包的,期望钱数都应该是一样的。现在让我们看看小蓝的草稿纸:
<小蓝的草稿纸>
对于第n个人,记其获得的钱数占红包总钱数的比例服从概率分布f n ( x ) f^n(x) f n ( x ) E n ( x ) E^n(x) E n ( x ) g n ( x ) ( x ∈ ( 0 , 1 ) ) g^n(x)(x\in(0,1)) g n ( x ) ( x ∈ ( 0 , 1 ) )
f 1 ( x ) = 1 , E 1 ( x ) = 1 2 , g 1 ( x ) = 1 f^1(x)=1, E^1(x)=\frac{1}{2}, g^1(x)=1
f 1 ( x ) = 1 , E 1 ( x ) = 2 1 , g 1 ( x ) = 1
啊,从第一步就开始不对了呢…
按照均匀分布的假设,第一个人平均会获得一半的钱。的确均匀分布就该是这样。直觉地猜测下去,第二个人平均会获得1 2 2 \frac{1}{2^2} 2 2 1 n n n 1 2 n \frac{1}{2^n} 2 n 1
不过看看这个“拼手速红包”会有怎样的性质呢?
<小蓝的草稿纸>
下面建立g n ( x ) g^n(x) g n ( x ) f n + 1 ( x ) , g n + 1 ( x ) f^{n+1}(x),g^{n+1}(x) f n + 1 ( x ) , g n + 1 ( x )
对于f n + 1 ( x ) f^{n+1}(x) f n + 1 ( x ) n + 1 n+1 n + 1 x x x t > x t>x t > x g n ( t ) g^n(t) g n ( t ) n + 1 n+1 n + 1 t t t x x x 1 t \frac{1}{t} t 1 t > x t>x t > x
f n + 1 ( x ) = ∫ x 1 g n ( t ) t d t f^{n+1}(x)=\int^1_x{\frac{g^n(t)}{t}dt}
f n + 1 ( x ) = ∫ x 1 t g n ( t ) d t
对于g n + 1 ( x ) g^{n+1}(x) g n + 1 ( x ) n + 1 n+1 n + 1 x x x t > x t>x t > x g n ( t ) g^n(t) g n ( t ) n + 1 n+1 n + 1 t t t ( t − x ) (t-x) ( t − x ) 1 t \frac{1}{t} t 1
g n + 1 ( x ) = ∫ x 1 g n ( t ) t d t = f n + 1 ( x ) g^{n+1}(x)=\int^1_x{\frac{g^n(t)}{t}dt}=f^{n+1}(x)
g n + 1 ( x ) = ∫ x 1 t g n ( t ) d t = f n + 1 ( x )
f n ( x ) f^n(x) f n ( x ) g n ( x ) g^n(x) g n ( x ) f n ( x ) f^n(x) f n ( x )
<小蓝的草稿纸>
由此我们得到f n ( x ) f^n(x) f n ( x )
f n + 1 ( x ) = ∫ x 1 f n ( t ) t d t f^{n+1}(x)=\int^1_x{\frac{f^n(t)}{t}dt}
f n + 1 ( x ) = ∫ x 1 t f n ( t ) d t
故f 2 ( x ) = ∫ x 1 1 t d t = − l n ( x ) , f 3 ( x ) = ∫ x 1 − l n ( x ) t d t = 1 2 l n 2 ( x ) f^2(x)=\int^1_x{\frac{1}{t}dt}=-ln(x), f^3(x)=\int^1_x{\frac{-ln(x)}{t}dt}=\frac{1}{2}ln^2(x) f 2 ( x ) = ∫ x 1 t 1 d t = − l n ( x ) , f 3 ( x ) = ∫ x 1 t − l n ( x ) d t = 2 1 l n 2 ( x )
可以看出,1 t \frac{1}{t} t 1
f n ( x ) = ( − l n ( x ) ) n − 1 ( n − 1 ) ! f^n(x)=\frac{(-ln(x))^{n-1}}{(n-1)!}
f n ( x ) = ( n − 1 ) ! ( − l n ( x ) ) n − 1
对于期望E n ( x ) = ∫ 0 1 x f n ( x ) d x E^n(x)=\int^1_0{xf^n(x)dx} E n ( x ) = ∫ 0 1 x f n ( x ) d x D n ( x ) = ∫ 0 1 ( x − E n ( x ) ) 2 f ( x ) d x D^n(x)=\int^1_0{(x-E^n(x))^2f(x)dx} D n ( x ) = ∫ 0 1 ( x − E n ( x ) ) 2 f ( x ) d x
E n ( x ) = 1 2 n , D n ( x ) = 1 3 n − 1 4 n E^n(x)=\frac{1}{2^n}, D^n(x)=\frac{1}{3^n}-\frac{1}{4^n}
E n ( x ) = 2 n 1 , D n ( x ) = 3 n 1 − 4 n 1
“呼~”,小蓝松了一口气,“还是蛮简单的嘛”
啊,还真的是非~常~简~单呢
“我编个程模拟一下,马上就好!”,小蓝从背包中翻出了笔记本。
小蓝编程的时候,我们来回顾一下数学的结果。f n ( x ) f^n(x) f n ( x ) l n n − 1 ( x ) ln^{n-1}(x) l n n − 1 ( x ) n n n
呀,小蓝已经编好了。
<小蓝的笔记本>
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import numpy as npfrom numpy import randomimport matplotlib.pyplot as pltnum = 100000 numinbin = 1000 lineplotnum = 1000 x = np.linspace(0 , 1 , lineplotnum) y = np.ones(lineplotnum) tmp = -np.log(x) leave = np.ones(num) for i in range (3 ): get = random.random(num) * leave leave -= get plt.figure() plt.hist(get, int (num / numinbin), density=1 ) plt.plot(x, y) y *= tmp / (i + 1 ) plt.show()
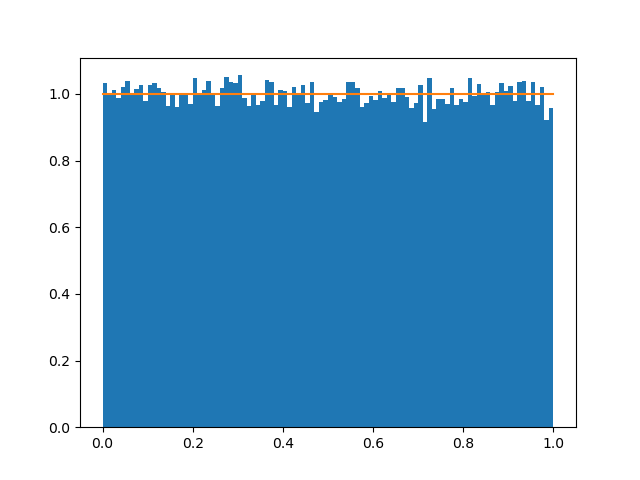
第一个抢红包的人
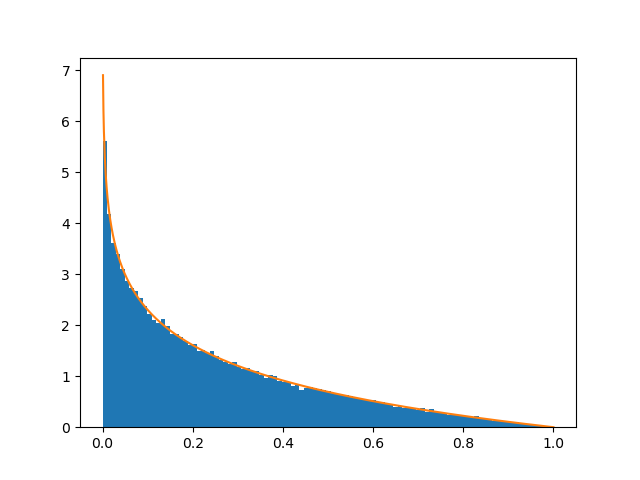
第二个抢红包的人
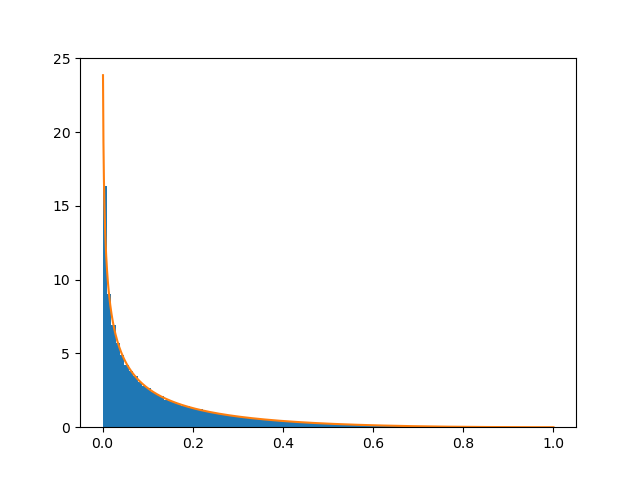
第三个抢红包的人
“做了十万次抢红包模拟得到的前四个人获得红包金额比例的频率直方图,和我推导出的橙色的概率密度曲线是贴合的!”小蓝自信地指着屏幕。
果然小蓝还是在这个时候最自信。应该说,真不愧是他。
“做了这么多关于红包的分析,过年的时候要给我包超大的红包哦。”我笑着看着小蓝。
“欸欸欸欸这有什么关系吗?!”
又是快乐的一天呢
总结一下,如果每次抢红包获得的金额都服从0到剩余所有金额的均匀分布,那么第n个人获得金额占总金额的比例服从( − l n ( x ) ) n − 1 ( n − 1 ) ! \frac{(-ln(x))^{n-1}}{(n-1)!} ( n − 1 ) ! ( − l n ( x ) ) n − 1 1 2 n \frac{1}{2^n} 2 n 1 1 3 n − 1 4 n \frac{1}{3^n}-\frac{1}{4^n} 3 n 1 − 4 n 1
出现错误的原因,主要还是因为第一个抢红包的人所获得的期望金额比例达到了1 2 \frac{1}{2} 2 1 1 n \frac{1}{n} n 1
https://www.bilibili.com/video/BV1z7411e7qB?from=search&seid=18007488927709895164